Der Weg zum automatischen Zehnerübertrag

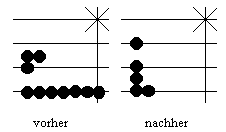	Bei der Arbeit am Rechenbrett muss der Rechner selbst erkennen, wann in einer Spalte zu viel Rechenmarken liegen. In diesem Fall tauscht er z.B. nach Abschluss der Rechnung fünf Marken an der Einerlinie gegen eine Marke im Fünferzwischenraum und zwei  Fünfzigermarken gegen eine Hundertermarke aus. Ähnlich verhält es sich beim Abakus. Hier kann der Benutzer die Rechnung 5+8 von vornherein nur dadurch ausführen, dass er in der Zehnerstelle eine Kugel hinzufügt und in der Einerstelle zwei Kugeln wegnimmt.
	Bei einfachen Bandaddierern wie dem Bassett Adder besitzt jedes umlaufende Band auf der linken Seite einen Haken, der beim Übergang von der 9 zur 0 in der nächsthöheren Stelle ein Warnsignal einblendet. In dieser Stelle ist dann entweder eine 1 einzugeben oder bei der Eingabe in diese Stelle zusätzlich 1 zu addieren.
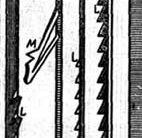	Schon im 16. Jahrhundert hatte es indes einen Rechner gegeben, der Überträge automatisch berücksichtigt. Bei "Abaque Rhabdologique" von Claude Perrault, einem Vorläufer der Zahlenschieber, besaß jede Stellenstange links einen gefederten Haken M, der in einen Zahn L der benachbarten Stellenstange eingriff und diese um eine Position weiterschob.
	Beim Addiator wird dem Rechner diese Denkarbeit abgenommen: Ist der Schieber neben der zu addierenden Zahl weiß, so kann er sie nach unten ziehen. Sieht der Rechner aber rot, so muss er den Schieber nach oben bewegen und wird durch die Führung dazu gezwungen, die höhere Stelle um eins zu erhöhen. Bei Überträgen über mehrere Stellen hinweg zeigt der Addiator einen roten Pfeil. Der Benutzer muss dann die nächste Zahnstange ganz hochziehen.
	Beim Stephenson-Adder funktioniert der Übertrag automatisch - über eine Stelle . Dafür sind erforderlich: Ein Zahnrad mit einem Zahn, eins mit zwanzig Zähnen, eine Klinke und eine Feder. Genial einfach, aber in der Praxis etwas rucklig und kaum auf mehrere Stellen auszuweiten. Außerdem funktioniert der Mechanismus nur in einer Richtung. Subtrahieren geht nicht.
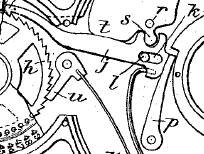	Einen schon raffinierteren automatischen Übertragsmechanismus von der Zehner- zur Hunderterstelle enthält der Webb Adder.  Sobald die große Scheibe eine Umdrehung gemacht hat, springt der lange Hebel nach rechts und zieht dabei die kleine Scheibe um einen Zahn weiter. Wichtig dabei ist, dass der Hebel erst im entscheidenden Moment in das Zahnrad eingreift. Vorher und nachher soll das kleine Zahnrad beweglich bleiben. "Schaltklinken" nach Art des gezeigten Hebels konnten Zahnräder auch um mehrere Positionen weiterdrehen. Man findet sie später auch in der Adix oder - auf Innenzahnungen einwirkend - in den Hamann-Vierspeziesmaschinen.
	Das erste Gerät mit automatischem Zehnerübertrag über mehrere Stellen erfand im 17. Jahrhundert der Tübinger Theologe Wilhelm Schickard. In seiner "Rechenuhr" waren die Ziffern 0 bis 9 auf einer runden Scheibe angeordnet. Eine Zahnradkonstruktion bewirkte, dass sich bei einer Umdrehung des Rades in der Einerstelle das Rad der Zehnerstelle um eine Position fortbewegte. Die nebenstehende Abbildung zeigt eine Version dieser Mechanik aus dem Addometer. Noch besser zu erkennen ist die Funktionsweise beim Seethroughcalc. Herausragend bei dieser Konstruktion ist, dass der Übertrag vorwärts und rückwärts funktioniert, dass also Subtraktionen durch Rückwärtsdrehen der Zahnräder möglich sind.
	Schickards Maschine ist nicht als Modell, sondern nur in einigen Zeichnungen enthalten. Wenige Jahre danach ließ Blaise Pascal einige Exemplare einer von ihm erfundenen Addiermaschine herstellen, die zuverlässig funktionierte, deren Zahnräder aber aufgrund einer komplizierten Übertragskonstruktion nur in einer Richtung bewegt werden konnten. Auf der Website von Pierre Charre kann man den Ablauf eines Zehnerübertrags bei einer Pascaline-Reproduktion in einem Quicktime-Film beobachten. Dies trifft auch auf den nebenstehend abgebildeten Mechanismus des Calcumeter zu, der 1901 für J. J. Walsh patentiert wurde.
	Bei späteren Konstruktionen sind die Zahlenscheiben häufig in die Vertikale gedreht und auf eine gemeinsame Achse gesteckt. Die Übertragungszahnräder sitzen auf einer zweiten, manchmal aber auch auf derselben Achse. Die Abbildung zeigt den Übertragsmechanismus aus der Wolverine Adding Machine, einem billigen Bleichspielzeug. Die Stellung der Zahlscheibe ganz rechts wird über das große Zahnrad auf ein Zahnrad im Inneren der weiß-roten doppelten Blechscheibe ganz rechts übertragen. Diese ist mit einer zweiten Doppelscheibe (Mitte) gekoppelt. In dieser sitzt nur ein einziger Zahn, der bei einer vollen Umdrehung der Doppelscheibe das kleine Zahnrad und damit die Zehner-Zahlenscheibe um eine Position weiterdreht.
	Dies ist der Mechanismus im Fallzähler. Durch eine doppelte Sperrklinke wird das rechte Zahnrad bei jedem Tastendruck um eine Position weitergedreht. auf der linken Seite des Einerrads befindet sich der Einzahn, der über das Übertragungszahnrad bei jedem zehnten Schritt das Zehnerrad um eine Position weiterbewegt. Eine Raste und eine Blattfeder sorgen bei dieser Bewegung dafür, dass das Zehnerrad nicht unbeabsichtigt überschleudert.
	Einzelne Konstruktionen wie der abgebildete Währungsrechner BriCal besaßen auch einen Übertrag zwischen konzentrischen Ringen.

Rechenwerkzeug.de